函数式编程通俗简介

函数式编程（functional programming）是一种与面向对象编程和过程式编程并列的编程范式。函数式编程来源于数学学科，因此有很多的数学理论方面的约束，但同时也得益于数学性框架带来的种种好处。很多初学者在接触函数式编程时都会感觉不适应，认为函数式编程很抽象，学习成本很高。本文试图通过一种通俗易懂的方式，来向大家介绍函数式编程是什么，以及更重要的，我们为什么要用函数式编程。

从初中数学入手

函数式编程来源于一门叫范畴论（category theory）的数学分支。范畴论这门学科同样也是很抽象的，因此，我们不直接从范畴论入手。但范畴论作为一门数学学科，它跟其它数学学科一样使用普遍的数学定义，遵从一般的数学定理。从这些我们已经熟知的数学定义和定理入手，会使学习函数式编程更简单，理解更深刻。

我们先来回顾一下初中数学函数的定义（下面的定义来自于维基百科）：

函数在数学中为两集合间的一种对应关系：输入值集合中的每项元素皆能对应唯一一项输出值集合中的元素。

关于这个数学函数的定义有两个特点要强调一下:

• 函数的输入只有一个元素，或者说函数的输入参数只有一个
• 对于相同的输入，函数的输出总是固定不变的，不管函数执行几次

在函数式编程里，我们使用的函数与数学函数一样，同样满足以上两个特点。你可能会认为第一个特点的限制太严格了，通常在编程里的函数都有好几个参数，如果限制一个参数我们的函数会很不灵活。我们将在后面介绍如何解决这个问题，下面我们先来看第二个特点。

纯函数

我们把满足上面第二个特点的函数称作纯函数（pure function）：

纯函数是这样一种函数，即相同的输入，永远会得到相同的输出，而且没有任何可观察的副作用。

这里的副作用（side effect）包含但不限于以下几种情况：

• 访问磁盘文件，包括数据库
• 发起网络请求
• 使用全局变量
• 修改任意变量的值，包括输入参数
• 刷新界面或打印日志

可以说，任何与函数外部的东西打交道都是不允许的，外部的信息只能通过参数传进函数，同样的，函数只能通过输出将信息传出到外部。

你可能会觉得很不可思议，如果连读写磁盘，发起网络请求，刷新界面这些都不可以，那么这个程序还有什么意义。实际上，函数式编程并不是不允许这些，而是强调要把这些副作用隔离开，我们将在后面简单提及用什么方法来解决。

使用纯函数带来很多好外：

• 可缓存性：对于同样的输入，输出是固定的，因此我们可以把输出结果缓存起来，避免重复计算。
• 可移植性：函数不依赖任何外部的东西，跟外部没有任何耦合。
• 可测试性：函数的运行结果不依赖于任何外部环境，完全由输入参数决定。
• 可并发性：函数不访问任何公共变量或公共资源，没有资源竞争的问题。

复合函数

我们来复习第二个数学定义，复合函数（同样来自维基百科）：

给定两个函数f : X → Y和g : Y → Z，其中f的陪域等于g的定义域（称为f、g可复合），则其复合函数，记为g ∘ f，以X为定义域，Z为陪域，并将任意x∈X映射为g(f(x))。有时也省略复合记号“∘”，直接写作g f。

在函数式编程的世界里，构建程序其实就是在合成函数。通过把一些功能单一的可复用的纯函数合成复杂的函数，以此完成复杂的任务。因此，我们需要一个方法来合成函数（以Javascript代码为例）：

var compose = function(f, g) {
  return function(x) {
    return f(g(x));
  };
};

函数的复合满足结合律：若f、g可复合，g、h可复合，则有：

h ∘ (g ∘ f) = (h ∘ g) ∘ f

即：

compose(f, compose(g, h));
// equal
compose(compose(f, g), h);

由于上述两种组合方式产生的函数是一样的，为了使用更方便简洁，我们有必要把compose方法扩展一下，以使它接受任意多的函数作为参数：

compose(f, g, h);

柯里化

上面我们遗留了一个问题，函数式编程里的函数接受的参数只能有一个，而我们实际项目中已经存在很多有用的函数，它们接受多个参数。我们如何在函数式编程里复用这些多个参数的函数呢？

这里要用到一个叫柯里化（currying）的概念。不要被这个名字吓到，其实柯里化的原理很简单：只传递给函数一部分参数，并生成一个新的函数去处理剩下的参数。而且有很多库已经实现了curry函数：

var curry = require('lodash/curry');

var match = curry(function(what, str) {
  return str.match(what);
});

match(/\s+/g, 'hello world');
// [ ' ' ]

match(/\s+/g)('hello world');
// [ ' ' ]

声明式编程方式

是时候看一个实际的例子。假设下面的prop，split函数是经过柯里化的（很多库已经提供这样的函数），我们可以看到，在合成isFirstNameFourLetter函数时，我们就像是在拼接管道（pipe）一样把一个个的函数拼接起来。而当我们给予isFirstNameFourLetter参数数据并调用它时，数据就会依次流过管道的每个结点并转换成我们想要的结果。

var head = function(x) {
  return x[0];
};
var strLength = function(x) {
  return x.length;
};
var isFourLetter = function(x) {
  return x === 4;
};

var isFirstNameFourLetter = compose(isFourLetter, strLength, head, split(' '), prop('name'));

isFirstNameFourLetter({
    name: 'Jon Snow'
});
// false

函数式编程就是这样的声明式（declarative）的编程方式。在函数式编程里，我们大多数时候是在拼接管道，希望数据流过管道后转变成我们想要的结果。与之相对应的，是命令式（imperative）的编程方式，在命令式的编程方式里，我们的思维是紧跟着程序指令的执行顺序的，我们在告诉计算机，先执行A指令，再执行B指令。

如果你用过SQL，或者是UNIX命令的管道，你可能已经感受到了声明式编程的优势。

Functor

到目前为止，我们的函数式编程有很多任务还是完成不了，比如下面这些：

• 条件分支
• 异常处理
• 读写磁盘
• 网络请求
• 异步任务

我们来看一个最简单的例子，假如我们在调用上面的isFirstNameFourLetter函数时，传进的参数不包含name属性，运行该函数会怎样？你可以试一下，在执行prop('name')时，会返回undefine，执行split(' ')时会抛异常。

我们的纯函数跟我们的管道只能有一个输入和一个输出，我们怎么处理这种异常的分支呢？为此，我们引进一个容器类Maybe，来作为流经我们管道的数据类型。

var Maybe = function(x) {
  this.__value = x;
};

Maybe.of = function(x) {
  return new Maybe(x);
};

Maybe.prototype.isNothing = function() {
  return (this.__value === null || this.__value === undefined);
};

Maybe.prototype.map = function(f) {
  return this.isNothing() ? Maybe.of(null) : Maybe.of(f(this.__value));
};

我们对Maybe内的数据的所有操作，都要通过map方法把纯函数传进Maybe容器里。而map方法的返回，依然是Maybe实例。我们可以像下面这样直接拼接管道并运行：

Maybe.of({
    name: 'Jon Snow'
}).map(prop('name')).map(split(' ')).map(head).map(strLength).map(isFourLetter);
//=> Maybe(false)

Maybe.of({
    nickname: 'Jon Snow'
}).map(prop('name')).map(split(' ')).map(head).map(strLength).map(isFourLetter);
//=> Maybe(null)

像Maybe这样的容器类，我们称之为functor:

functor 是实现了 map 函数并遵守一些特定规则的容器类型。

学习函数式编程，很多时候就是在学习各种各样的functor：

• Maybe：外理null，undefined等边界情况
• Either：处理异常错误
• IO：处理磁盘读写
• Task：处理异步任务
• Stream：处理事件流

要把这些functor讲清楚，我们同时需要了解monad概念，由于本文的篇幅原因，这里不作详述。但我相信，如果你已经找到函数式编程的感觉，学习这些functor并不是一件难事。

范畴论

接下来，我们来了解一下函数式编程的来源，范畴论（category theory）。范畴论是一门很抽象的数学分支，范畴论希望通过统一的形式来处理其它多门数学分支，如集合论（set theory），逻辑学（logic）等等。

在范畴论里，范畴（category）包含以下几个部分：

• 对象集：一个例子是类型String，Boolean，Number，Object等的所有可能取值的集合。
• 态射集：态射即纯函数，或者说是对象之间的有向边，一个对象通过态射可以映射到同一范畴里的另一个对象。
• 态射合成的概念：即函数合成的概念。
• identity态射：一个特殊的态射，任何对象经过该态射总是映射回自己。

范畴论里的另一个重要的概念就是functor。functor把一个范畴映射到另一个范畴，且保持了原范畴的网络结构。

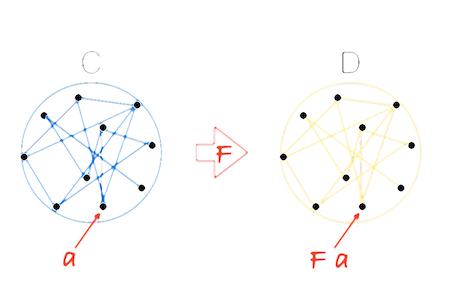
如上图所示，原范畴C里的对象a，经过functor F映射后变成范畴D里的对象Fa（例如Maybe.of(a)），而原范畴里的任一态射f，经过functor F映射后变成范畴D里的新态射map(f)。

范畴论之所以能用统一的形式处理其它数学分支，在于范畴里的对象集可以是许多抽象的东西。比如用范畴论处理集合论时，对象可以是集合，而态射是集合间的函数。范畴里的对象甚至可以是另一个范畴，这也是范畴论抽象的原因。

最后

至此，我们已经看到了函数式编程带来的种种好处。比如纯函数的可缓存性，可移植性，可测试性和可并发性。再比如声明式编程方式使编程站在一个更高的抽象层面，而不必去关心指令级别的细节。除此之外，函数式编程还得益于范畴论的许多数学定理。我们来看一个简单的例子：

compose(map(f), map(g)) === map(compose(f, g));

从这个定理我们知道，一个对象经过复合函数compose(f, g)的转换再映射到另一个范畴等价于先映射到另一个范畴再经过复合函数compose(map(f), map(g))的转换。为此，我们可以找出其中较优的路径（性能更高）来实现同一个需求。这种优化可以在底层实现而做到对开发者透明。就好比我们的数据库引擎升级了，但我们的SQL不用做任何改动。

这只是范畴论众多有用的定理中的一个。本文限于篇幅，不能一一缀述，有兴趣的读者可以自己上网查阅。